Rekenen met breuken
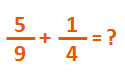
Net als hoofdrekenen kunnen rekensommen met breuken onderdeel uit maken van een assessment of intelligentie test. Op deze pagina leer je binnen een uur de meest gangbare bewerkingen met breuken oplossen. We behandelen het optellen, aftrekken, vermenigvuldigen en delen van twee breuken.
Wat zijn breuken
Een breuk is niet meer dan een getal gedeeld door een ander getal. Een breuk wordt meestal geschreven in verticale vorm, waarbij het getal boven de streep de teller wordt genoemd, en het getal onder de streep te noemer. Op deze pagina schrijven we een breuk ook in de vorm van T/N, waarbij T de teller is en N de noemer, bijvoorbeeld 2/3 of 6/14.

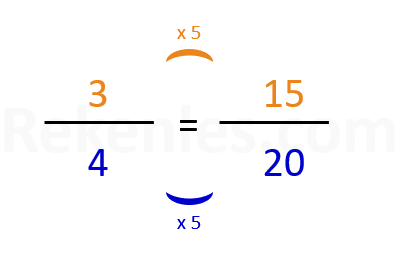
Een belangrijke eigenschap van breuken is dat je de teller en de noemer altijd tegelijk met hetzelfde getal mag vermenigvuldigen. Stel je vermenigvuldigt de teller en noemer uit de breuk 3 /4 met het getal 5. Je krijgt dan 15 / 20. Het is belangrijk om te weten dat je dit met alle breuken en alle getallen kunt doen.
Hetzelfde geldt voor delen: als je de teller en noemer door hetzelfde getal deelt, zal de breuk altijd hetzelfde blijven. Stel we delen de teller en de noemer uit de breuk 8/20 door het getal 4. De uitkomst is dan 2/5, en dat is precies hetzelfde als 8/20. Dit geldt altijd en in alle gevallen.
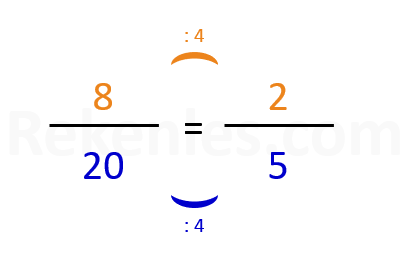
Deze twee principes zijn belangrijk in het optellen en aftrekken van twee breuken, en vormen de basis voor deze bewerkingen.
Het vereenvoudigen van een breuk is simpelweg het herschrijven van een breuk naar een kleinere teller en een kleinere noemer. Zo kun je bijvoorbeeld 4/20 vereenvoudigen tot 1/5, en 21/33 tot 7/11. Dit kun je snel doen met behulp van het algoritme van Euclides.
Optellen
Je kunt twee breuken alleen bij elkaar optellen als ze beide dezelfde noemer hebben. De optelling is dan eenvoudig: je telt simpelweg de tellers bij elkaar op.
Kijk maar naar de volgende voorbeelden:
Voorbeeld: 2/5 + 1/5 = ?
3/5 (beide breuken hebben dezelfde noemer, dus mag je de tellers bij elkaar optellen)
Het wordt ingewikkelder als de breuken niet dezelfde noemer hebben. Je moet dan zorgen dat de noemers hetzelfde worden. Zoals je aan het begin van deze pagina hebt gelezen mag je de teller en de noemer altijd met hetzelfde getal vermenigvuldigen. We gebruiken deze eigenschap om de noemers van de twee breuken aan elkaar gelijk te maken:
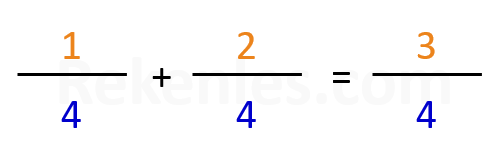
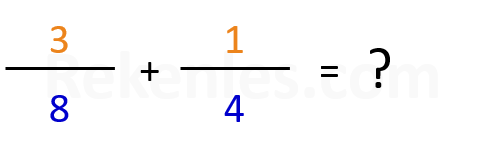
Voorbeeld: 1/4 + 3/8 = ?
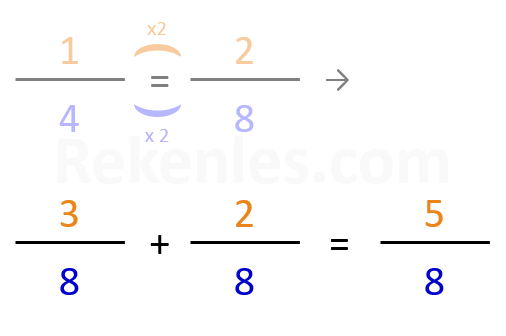
1/4 = 2/8 (je mag de teller en de noemer altijd met hetzelfde getal vermenigvuldigen. In dit geval vermenigvuldigen we beiden met 2)
2/8 + 3/8 = 5/8 (als de noemers gelijk zijn, mag je de tellers bij elkaar optellen - zie het vorige voorbeeld)
Het meest ingewikkeld is de optelling waarbij beide breuken een verschillende noemer hebben, en die je allebei moet vermenigvuldigen om de noemer gelijk te krijgen. Je moet dan zoeken naar het eerst volgende getal dat je kunt delen door zowel de noemer van het eerste getal, als de noemer van het tweede getal. De noemer waarvoor dit geldt, wordt ook wel de kleinste gemene deler genoemd.
Voorbeeld: 1/5 + 2/7 = ?
1/5 = 7/35 (we vermenigvuldigen de teller en de noemer met 7. Let op: 7 is de noemer van de tweede breuk)
2/7 = 10/35 (we vermenigvuldigen teller en noemer met 5)
7/35 + 10/35 = 17/35 (nu de noemers gelijk zijn kunnen we de noemers simpelweg bij elkaar optellen
Aftrekken
Het aftrekken met breuken is bijna hetzelfde als het optellen. Net als bij het optellen van breuken, kun je breuken alleen van elkaar af trekken als ze dezelfde noemer hebben:
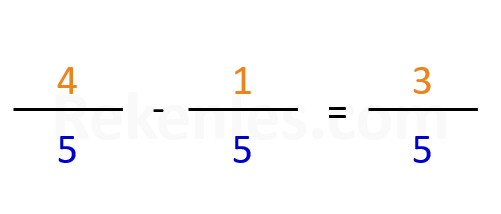
Voorbeeld: 4/5 - 1/5 = ?
3/5 (beide breuken hebben dezelfde noemer, dus we mogen de tellers van elkaar af trekken)
Als de breuken niet dezelfde noemer hebben, moet je de noemers eerst aan elkaar gelijkmaken. Dat doe je – net als bij het optellen van breuken – door de breuken te vermenigvuldigen met hetzelfde getal. In de volgende voorbeelden doen we dat voor:
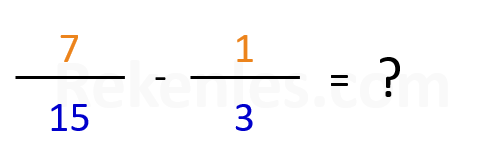
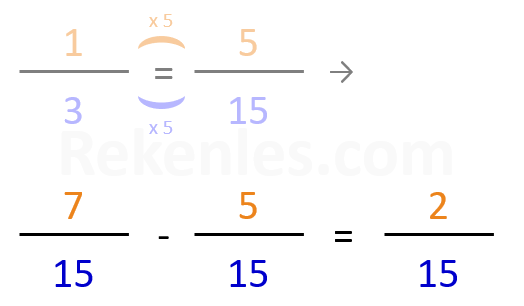
Voorbeeld: 7/15 - 1/3 = ?
1/3 = 5/15 (we vermenigvuldigen de teller en de noemer met het getal 5, zodat de noemers aan elkaar gelijk zijn)
7/15 - 5/15 = 2/15 (nu de noemers aan elkaar gelijk zijn, trekken we de tellers van elkaar af)
Vermenigvuldigen
We beginnen met het vermenigvuldigen van een breuk met een geheel getal. Dat is makkelijk: je vermenigvuldigt simpelweg de teller met het gehele getal.
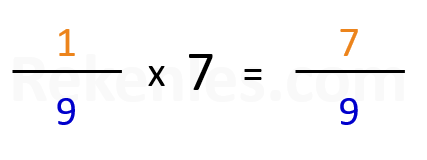
Voorbeeld: 1/9 x 7 = ?
7/9 (de teller wordt vermenigvuldigd met het hele getal)
Het principe van het vermenigvuldigen van breuken is eenvoudig: je vermenigvuldigt de teller met de teller, en de noemer met de noemer. Als je dat gedaan hebt, kun je de uitkomst in sommige gevallen weer vereenvoudigen.
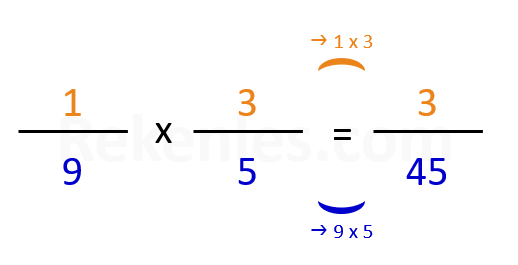
Voorbeeld: 1/9 x 3/5 = ?
vermenigvuldig te teller met de teller: 1 x 3 = 3
vermenigvuldig de noemer met de noemer: 9 x 5 = 45
uitkomst = 3/45
Let op: 3/45 kun je vereenvoudigen tot 1/15 door de teller en noemer beiden te delen door 3.
Delen
De moeilijkste bewerking met breuken is het delen van breuken. We beginnen met een eenvoudig voorbeeld. Stel we delen het getal 4 door 2. Dit zouden we kunnen zien als 4/1 : 2/1, en de uitkomst is natuurlijk 2. Stel we delen ¼ door twee. Dat is ook nog relatief eenvoudig: de uitkomst is 1/8. Dat kun je je nog als volgt voorstellen: je snijdt een taart in vieren, en daarna snijd je ieder van de parten weer door midden.
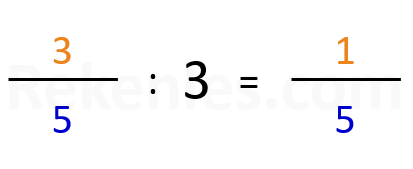
Het wordt ingewikkelder als we gaan delen door een getal dat kleiner is dan 1. Stel we delen het getal vier door 1/2. Ook als we de uitkomst niet weten, weten we wel dat hals we het getal waarnaar we op zoek zijn vermenigvuldigen met 1/2, de uitkomst van die vermenigvuldiging precies 4 is.
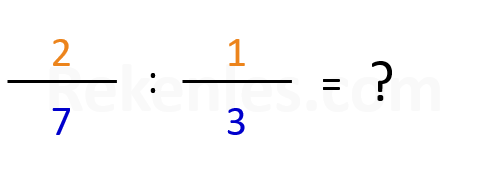
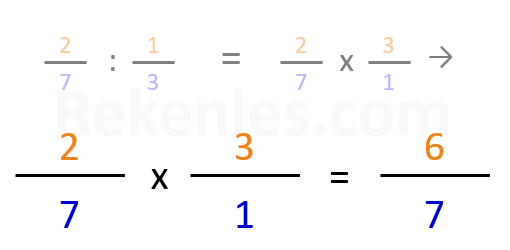
Kijk maar naar het volgende voorbeeld:
4 : 1/2 = ?
Deze som kun je ook schrijven als: ... x 1/2 = 4
Je weet dat de uitkomst 8 is, want 8 x 1/2 = 4
Zo geldt ook dat 4 : 1/2 = 8
Omdat dit bovenstaande geldt, wordt ook wel gezegd: "het delen door een breuk is hetzelfde als vermenigvuldigen met het omgekeerde". En dat klopt, want 7 : 1/2 is hetzelfde als 7 x 2/1, en 9 : 2/5 = 9 x 5/2.
Meer oefeningen
Wil je verder oefenen met breuken? Hier staan nog twaalf opgaven die je gratis kunt gebruiken. De antwoorden staan onderaan deze pagina.

Antwoorden
1. 2/3
2. 19/35
3. 15/10 = 1 5/10 (vereenvoudigd) = 1 1/2 (vereenvoudigd)
4. 1/4
5. 2/21
6. 2/9
7. 3/8
8. 12/35
9. 2/18 = 1/9 (vereenvoudigd)
10. 6/8 = 3/4 (vereenvoudigd)
11. 3/10
12. 6/5 = 1 1/5 (vereenvoudigd)
Rekenles.com 2018 ©

